图像基本变换
图像基本变换:缩放、平移、镜像、旋转、透视。
前言
本系列文章(DIP,Digital Image Processing),用于记录总结数字图像处理课程的实验内容。目录请参考DIP系列文章。
题目要求
- 图像缩放
- 图像平移
- 图像镜像
- 图像旋转
- 图像透视(选做就是不做)
原图(测试图像)
仅对8位灰度图进行处理,RGB真彩色处理同理。

整体思路
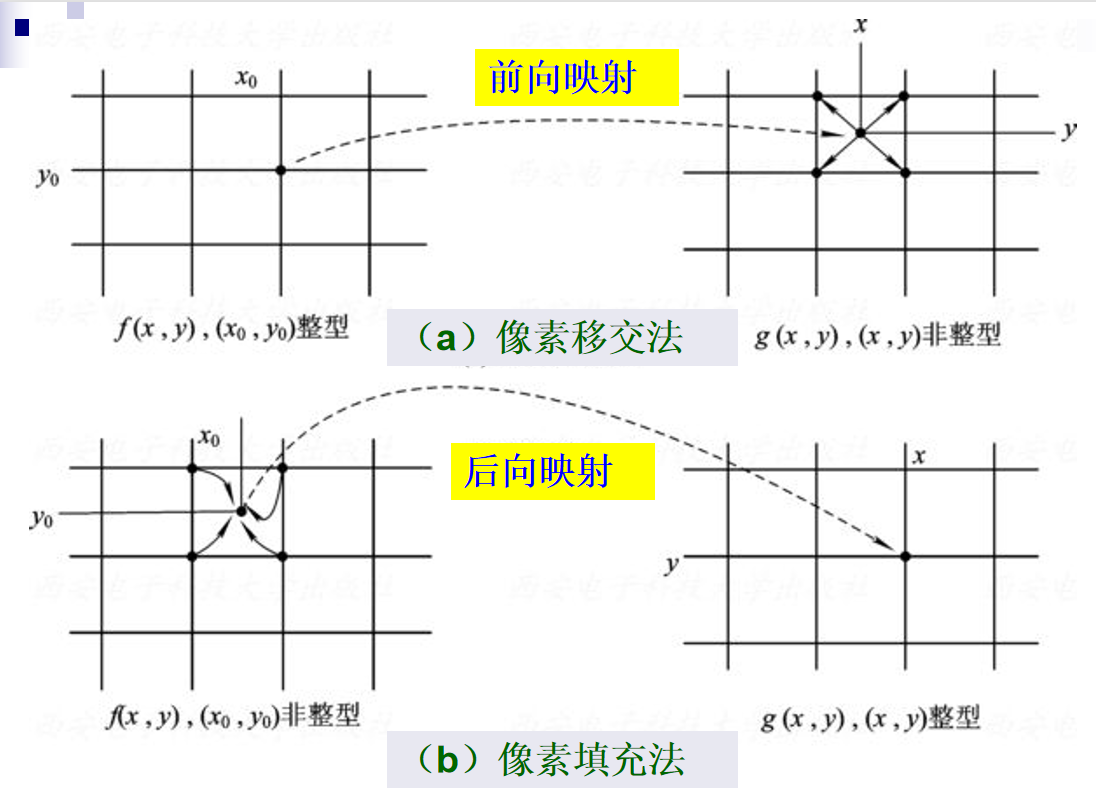
空间域处理都是对每个像素进行处理,无非就是做一层映射而已。
利用后向映射进行变换,即根据转换后图像的像素位置确定转换前的像素位置,得到像素灰度值并赋值给转换后图像像素。
实验内容
思路及效果如下:
0x00 基本变量表
| 变量名 | 含义 |
|---|---|
| $x_0 $ | 原像素横坐标值 |
| $y_0 $ | 原像素纵坐标值 |
| $x$ | 转换后横坐标值 |
| $y$ | 转换后纵坐标值 |
| $t_1$ | 转换幅度值,放缩倍数、平移量等 |
| $t_2$ | 转换幅度值,放缩倍数、平移量等 |
| $width $ | 图像水平像素个数 |
| $height$ | 图像垂直像素个数 |
| $\theta$ | 顺时针旋转角度 |
0x01 图像缩放
转换矩阵:
$$\left[
\begin{matrix}
x \\
y \\
1 \\
\end{matrix}
\right] =
\left[
\begin{matrix}
t_1 & 0 & 0 \\
0 & t_2 & 0 \\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x_0 \\
y_0 \\
1 \\
\end{matrix}
\right] $$
后向映射为:
$$\left[
\begin{matrix}
x_0 \\
y_0 \\
1 \\
\end{matrix}
\right] =
\left[
\begin{matrix}
\frac{1}{t_1} & 0 & 0 \\
0 & \frac{1}{t_2} & 0 \\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x \\
y \\
1 \\
\end{matrix}
\right] $$
这样即可求得转换后图像当前坐标的灰度值为多少了。
宽×3,高×4

0x02 图像平移
向左下平移
转换矩阵:
$$\left[
\begin{matrix}
x \\
y \\
1 \\
\end{matrix}
\right] =
\left[
\begin{matrix}
1 & 0 & t_1 \\
0 & 1 & t_2 \\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x_0 \\
y_0 \\
1 \\
\end{matrix}
\right] $$
后向映射为:
$$\left[
\begin{matrix}
x_0 \\
y_0 \\
1 \\
\end{matrix}
\right] =
\left[
\begin{matrix}
1 & 0 & -t_1 \\
0 & 1 & -t_2 \\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x \\
y \\
1 \\
\end{matrix}
\right] $$

0x03 图像镜像
只展示水平镜像,垂直同理。
转换矩阵:
$$\left[
\begin{matrix}
x \\
y \\
1 \\
\end{matrix}
\right] =
\left[
\begin{matrix}
-1 & 0 & width \\
0 & 1 & 0 \\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x_0 \\
y_0 \\
1 \\
\end{matrix}
\right] $$
后向映射为:
$$\left[
\begin{matrix}
x_0 \\
y_0 \\
1 \\
\end{matrix}
\right] =
\left[
\begin{matrix}
-1 & 0 & width \\
0 & 1 & 0 \\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x \\
y \\
1 \\
\end{matrix}
\right] $$
水平镜像

垂直镜像

0x04 图像旋转
转换矩阵:
$$\left[
\begin{matrix}
x \\
y \\
1 \\
\end{matrix}
\right] =
\left[
\begin{matrix}
\cos\theta & \sin\theta & 0 \\
-\sin\theta & \cos\theta & 0 \\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x_0 \\
y_0 \\
1 \\
\end{matrix}
\right] $$
后向映射为:
$$\left[
\begin{matrix}
x_0 \\
y_0 \\
1 \\
\end{matrix}
\right] =
\left[
\begin{matrix}
\cos\theta & -\sin\theta & 0 \\
\sin\theta & \cos\theta & 0 \\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x \\
y \\
1 \\
\end{matrix}
\right] $$
顺时针旋转45°

0x05 图像透视
没做。
不足
- 未对RGB真彩色图像做变换,原理一样,懒得做
- 未做透视变换
- 未使用线性插值方法进行补像素灰度值
总结
本次实验主要是熟悉图像的基本变换,如果文中有错误,欢迎在评论区指正。请继续关注DIP,数字图像处理系列文章!